Interest Rate Swaps Value Drivers for These Popular Hedging Tools
Interest Rate Swaps Value Drivers for These Popular Hedging Tools
With the widespread use of swaps and other derivatives with counterparty risk, firms must understand the valuation factors behind these financial instruments.
An interest rate swap is a contractual agreement between two parties to exchange interest payments, typically with fixed rate payments exchanged for floating rate payments. The interest rate swaps market is the largest derivative market in the world, with an estimated $311.5 trillion outstanding in notional amounts as of June 2016, according to the Bank of International Settlements. Interest rate swaps have become an essential tool for many companies to hedge against anticipated adverse movements in interest rates (i.e., they convert a floating rate liability into a fixed rate liability).
Derivative instruments, such as interest rate swaps, are carried at fair value, and according to generally accepted accounting principles (specifically, Financial Accounting Standard Board (FASB) Topic 820, Fair Value Measurement (FASB ASC 820)), the fair value measurement must include consideration of the effects of counterparty credit risk (i.e., nonperformance risk). Investment and commercial banks are usually the swap market makers and provide the markto- market value of interest rate swap contracts, but not the credit valuation adjustment (CVA). Also, model inputs used in swap analyses can substantially affect the fair value of the swaps. These factors have led to a need for thirdparty financial analysis to derive the value of such instruments. Accordingly, we focus on the accounting guidance for interest rate swaps and a valuation model used to analyze the fair value of an interest rate swap and the counterparty credit risk.
Overview of Interest Rate Swaps
Interest rate swaps are derivative instruments that trade over the counter. A plain-vanilla swap involves counterparties exchanging fixed rate cash flows and floating rate cash flows. The party paying the fixed rate is the “payer” and the party paying the floating rate is the “receiver.”
Corporations or investors generally enter into swap agreements with investment or commercial banks (the swap market makers). The floating rate is typically based on the London Inter-Bank Offered Rate (LIBOR), which is a benchmark rate banks charge each other for short-term loans, plus a spread. The value of the swap is the net amount between the fixed and floating payments. The notional principal amount on which the fixed and floating rates are based is never exchanged; only the interest payments are.
At the inception of the swap agreement, the terms of the swap are established such that the value of the swap is equal to zero (i.e., the present value of total fixed rate cash flows and floating rate cash flows implied by the forward LIBOR curve are equal). The two main risks associated with interest rate swaps are interest rate risk and counterparty credit risk. The value of the swap will change in subsequent periods as counterparty credit risk and forward expectations of the floating rate change.
Accounting Guidance
Under the guidance of FASB ASC 820, interest rate swaps must be reported at fair value for each reporting period. FASB ASC 820 is defined as the price that would be received to sell an asset or paid to transfer a liability in an orderly transaction between market participants at the measurement date. The counterparty credit risk associated with the liability needs to be accounted for in the price, with the rationale being that a buyer would pay less for an instrument with high credit risk. In that case, there is a risk that the contract will not be fulfilled as stated in the agreement, so the value of the swap, in most cases, is less.
Interest rate swaps are covered under the scope of FASB ASC Topic 815, Derivatives and Hedging (FASB ASC 815), which governs the rules of derivative instruments. Since interest rate swaps must be reported at fair value, this can lead to volatility in the income statement. A company can elect to apply hedge accounting to reduce this volatility, in which case the interest rate swap and the hedged item are reported as one entry. Interest rate swaps can be classified as fair value hedges or cash flow hedges. A fair value hedge is for recognized assets or liabilities (i.e., a company wants to hedge the fair value of a fixed rate loan with an interest rate swap by being the receiver). Under the fair value hedge, the gain or loss on the hedging instrument is recognized as current earnings. A cash flow hedge is for variable cash flows on recognized asset or liabilities (i.e., a company wants to hedge floating rates with an interest rate swap by being the payer). An effective cash flow hedge is initially reported as other comprehensive income, and reclassified as earnings when the hedge expires. Hedge accounting can make financial statements more straightforward by having fewer line items and reducing the volatility in the income statement introduced by derivative instruments.
Determining a Swap’s Fair Value
Interest rate swaps are valued using a discount cash flow analysis by taking the present value of the fixed and floating rate cash flows. The forward LIBOR curve and the counterparty’s credit risk can change over time; therefore, the calculations of the future cash flows and the present value factors, which include the CVA, are particularly important.
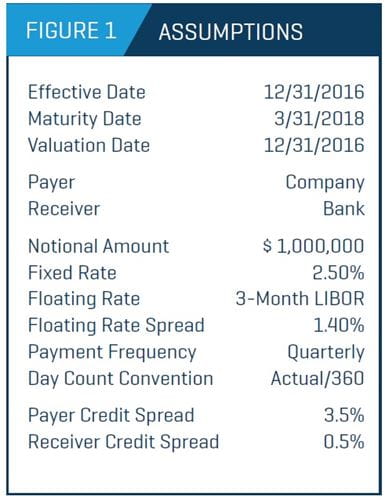
As seen in Figure 1, a bank and a company enter into an interest rate swap agreement on December 31, 2016, for a notional amount of $1.0 million. The company is the payer and pays a fixed rate of 2.50%. The bank is the receiver and pays 3-month LIBOR plus a spread of 1.40%. Interest payments are quarterly Actual/360. The agreement matures on March 31, 2018.
Determination of Cash Flows
The net future cash flows are calculated by determining the future payments for the payer and the receiver.
- Fixed payments: The future payments are a series of fixed payments based on an interest rate known at inception. Therefore, these cash flows are known and just need to be calculated based on the time between payments and the day count convention.
- Floating payments: The future payments are a series of variable payments based on the LIBOR forward curve. The LIBOR forward curve is derived from the LIBOR yield curve as of the valuation date. Since expectations of the LIBOR yield curve change over time, the LIBOR forward curve will change, as well.
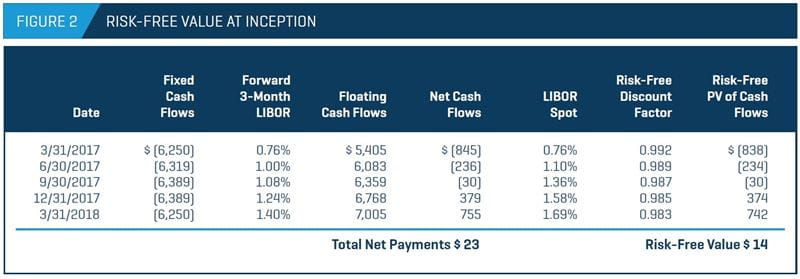
As shown in Figure 2, from the company’s perspective, the net payments are the floating payments (asset to the company) minus the fixed payments (liability to the company).
Fair Value of the Swap
At inception, the fair value of the interest rate swap is zero, which also incorporates the counterparty credit risk. There are several methods for estimating the counterparty credit risk, since it is not standardized and varies among market participants. The methods can range from very simple to very complex, driven by the sophistication and resources of the company and also by the purpose of the analysis. Complex approaches involve modeling and simulating interest rate volatilities, but for the purpose of financial reporting, simpler methods are usually sufficient.
The simplest approach is to calculate the risk free value of the derivative, and then repeat the calculation by adjusting the discount rates by the credit spread of the counterparty that is in the liability position. The counterparty risk adjustment (or CVA) can be calculated based on the remaining cumulative future cash flows for each payment date until maturity or based on each cash flow leg separately. In this example, we calculate the CVA based on the remaining cumulative future cash flows. If the aggregate future cash flows are an asset to the company, the bank’s CVA is used to calculate the discount rate. If the aggregate cash flows are a liability to the company, the company’s CVA is used.
Listed below are some methods appropriate for estimating the credit spread used in the CVA adjustment of public and private companies.
Public company
Credit default swap (CDS): A CDS is a swap in which the seller will compensate the buyer in the event of a default or credit event. Essentially, the buyer is purchasing insurance for a fixed income instrument. The price of the CDS is the spread. A higher spread would indicate higher risk and a higher default probability. Since the spread is indicative of the credit risk of the company, it is a good measure of the counterparty risk. However, CDS are not available for many entities, and if they are, they may have issues with liquidity.
Public debt: If a public company has public debt, the yield can be used to estimate a spread for the counterparty credit risk. The yield on the debt will imply a credit rating, but based on the seniority of the debt, the credit rating might have to be adjusted up or down. The yield used for the counterparty credit risk is then the yield implied by the concluded credit rating.
Credit rating: Based on the credit rating of the public company, a yield can be estimated using a rated composite yield curve or traded bond yields. A spread can be extracted by analyzing the difference between the rated yield and LIBOR. A higher-rated company will have a lower credit spread than a lower-rated company.
Private company
Private debt: If a private company has any recently issued debt, the yield of the debt can be used similarly to publicly traded debt as described above.
Proxy credit rating: If a private company has not recently issued debt, a fundamental analysis can be done to estimate the company’s credit rating. Several metrics can be used to analyze the company’s credit rating: interest coverage (i.e., earnings before interest and tax divided by interest expense), leverage (i.e., total debt divided by enterprise value), return on assets (i.e., net income divided by total assets), total assets, retained earnings divided by total assets, and cash and cash equivalents divided by total assets. The metrics of a universe of rated public companies can be estimated as well. The metrics of the company are then compared with the metrics of the universe of rated public companies to determine a proxy credit rating for the company.
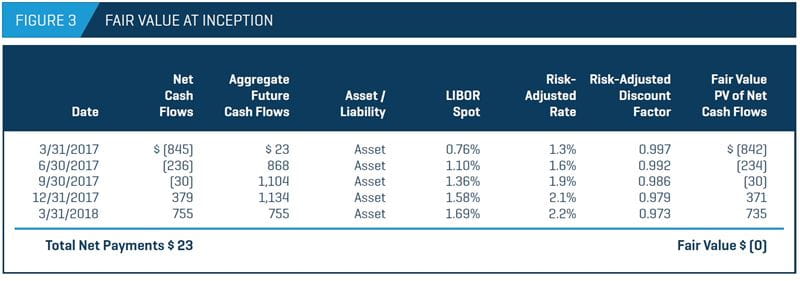
In this example, the company is assumed to have a credit spread of 3.50%, and the bank is assumed to have a credit spread of 0.50%. To determine the present value discount factor, the company’s or the bank’s credit spread is added to the LIBOR spot rate. At inception, the aggregate cash flows are an asset to the company, so the bank’s credit spread is used to calculate the discount factor. The fair value of the interest rate swap is then calculated by multiplying the risk-adjusted discount factor and the net cash flows. As shown in Figure 3, the fair value of the swap is zero at inception.
Although, historically, common practice has been to use LIBOR as part of the discount factor, the overnight index swap (OIS) rate has been used more frequently since the global financial crisis. An OIS is an interest rate swap in which an overnight rate, such as the federal funds rate, is being exchanged for a fixed rate. The OIS rate is typically considered less risky since it is indicative of interbank counterparty risk. With the use of collateralization in the interest rate swap market, interest rate swaps have become relatively low risk, and the OIS rate is more risk-free than LIBOR. The OIS rate is considered less risky than LIBOR because an OIS contract involves only the exchange of interest payments based on a notional principal amount, whereas a LIBOR loan requires the repayment of interest and principal. Use of the OIS curve to discount interest rate swaps better considers the economics of the derivative instrument and the relationship between the counterparties. However, there are still some practical issues with the use of the OIS curve in swap valuations, such as needing separate curves to estimate the floating payments and discount the cash flows.
Scenario Analysis
Among the key drivers of value are interest rates, since the future floating rates are unknown. Figure 4 shows two scenarios: interest rates increasing and interest rates decreasing at the next payment date. If interest rates increase by 25 basis points, the floating payments increase and the net payments result in a net asset for the company. If interest rates decrease by 25 basis points, the floating payments decrease and the net payments result in a net liability for the company. Therefore, depending on how the yield curve changes in subsequent measuring periods, a swap can become an asset or a liability for the company.
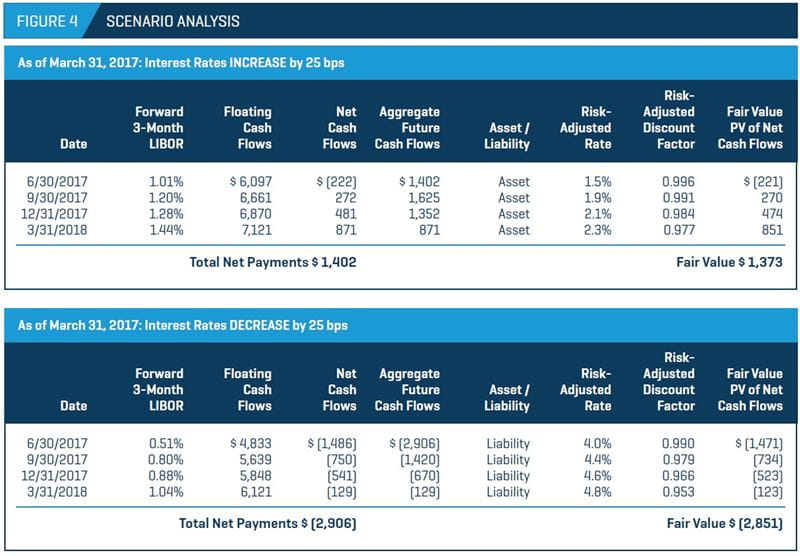
The counterparty credit risk can also affect whether the company reports a gain or a loss. If the interest rate swap is already a liability but the credit quality of the company deteriorates, the liability for the company will decrease and the company can report a gain. The opposite can also occur – the company can report a loss if its credit quality improves while all else remains the same.
Key Takeaways
Interest rate swaps have become a popular way for many types of companies to manage interest rate risk, especially with the current uncertainty in future interest rate movements. Companies can also use hedge accounting to limit the volatility in their income statements due to the interest rate swaps. To comply with current accounting standards, interest rate swaps must be reported at fair value, which requires analysis of sensitive inputs such as the forward yield curve and counterparty credit risk. The concepts presented here – determining cash flows from both legs and determining an appropriate CVA – can be applied to other types of swaps and derivative instruments, as well.
This is an updated version of an article published in the Spring 2010 issue of the Journal.




